앞장에서 word2vec의 구조를 배우고 CBOW모델을 구현했다. 하지만 말뭉치에 포함된 어휘 수가 많아지면 계산량도 커져, CBOW모델을 계산 시간이 너무 오래 걸린다는 단점이 있다.
그래서 이번 장의 목표는 word2vec의 속도 개선으로, 단순한 word2vec에 아래 두 가지 개선사항을 추가할 것이다.
1) Embedding이라는 새로운 계층 도입
2) 네거티브 샘플링이라는 새로운 손실 함수 도입

앞 장의 CBOW모델은 단어 2개를 맥락으로, 하나의 단어(타깃)를 추측한다. 이 때 입력 측 가중치(Win)와의 행렬 곱으로 은닉층이 계산되고, 다시 출력 측 가중치(Wout)와의 행렬 곱으로 각 단어의 점수를 구한다. 그리고 이 점수에 소프트맥스 함수를 적용해 각 단어의 출현 확률을 얻고, 이 확률을 정답 레이블과 비교하여(정확히는 교차 엔트로피 오차를 적용하여) 손실을 구한다.
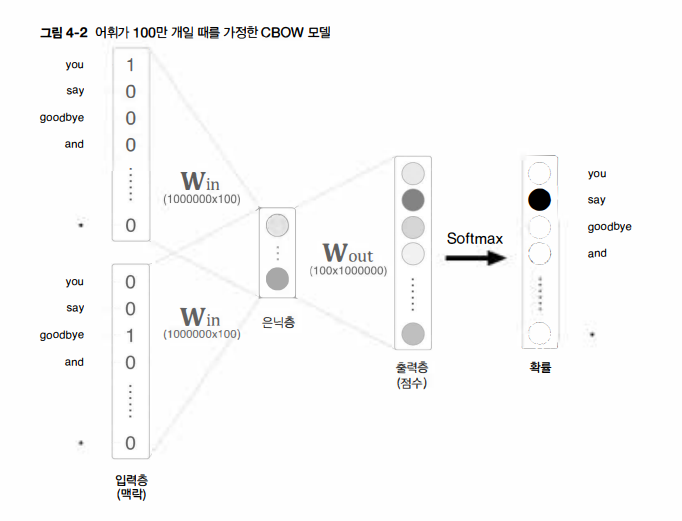
하지만 위 그림에서처럼 입력층과 출력층에는 각 100만 개의 뉴런이 존재한다고 가정하자면, 수많은 뉴런 때문에 중간 계산에 많은 시간이 소요된다. 정확히는 다음의 두 계산으로 병목현상이 일어난다.
1) 입력층의 원핫 표현과 가중치 행렬 Win의 곱 계산
2) 은닉층과 가중치 행렬 Wout의 곱 및 Softmax 계층의 계산
첫 번째는 입력층의 원핫 표현과 관련된 문제입니다. 단어를 원핫 표현으로 다루기 때문에 어휘 수가 많아지면 원핫 표현의 벡터 크기도 커지게 되는 것이다. 게다가 이 원핫 벡터와 가중치 행렬 Win을 곱해야 하는데, 이것만으로 계산 자원을 상당히 사용하게 되어 Embedding 계층이라는 것을 도입하게 된다.
두 번째는 은닉층 이후의 계산으로, 우선 은닉층과 가중치 행렬 Wout의 곱만 해도 계산량이 상당하다. 그리고 Softmax 계층에서도 다루는 어휘가 많아짐에 따라 계산량이 증가하는 문제가 있다. 이 문제는 네거티브 샘플링이라는 새로운 손실 함수를 도입해 해결할 수 있다.
4.1.1 Embedding 계층
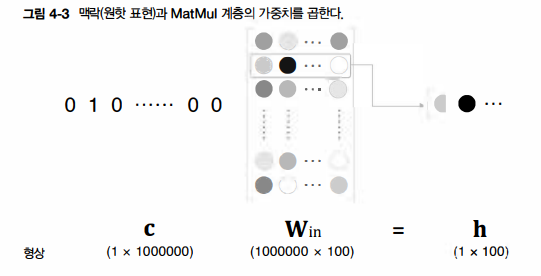
앞 장의 word2vec 구현에서는 단어를 원핫 표현으로 바꿔, MatMul 계층에 입력한 후 MatMul 계층에서 가중치 행렬을 곱했다. 만약 여기서 어휘 수가 100만개라면 행렬 곱은 위 그림처럼 된다. 거대한 벡터와 가중치 행렬을 곱해, 결과적으로 수행하는 일은 단지 행렬의 특정 행을 추출하는 것뿐이다. 따라서 원핫 표현으로의 변환과 MatMul 계층의 행렬 곱 계산은 사실 필요가 없다.
그럼 가중치 매개변수로부터 '단어 ID에 해당하는 행(벡터)'을 추출하는 계층을 만들어보자. 그 계층을 Embedding계층이라고 부르겠고, 즉 Embedding 계층에 단어 임베딩(분산 표현)을 저장하는 것이다.
4.1.2 Embedding 계층 구현
행렬에서 특정 행을 추출하기란 아주 쉽다. 예컨대 가중치 W가 2차원 넘파이 배열일 때, 이 가중치로부터 특정 행을 추출하려면 그저 W[2]나 W[5]처럼 원하는 행을 명시하면 끝이다.

또한 가중치 W로부터 여러 행을 한꺼번에 추출하려면, 원하는 행 번호들을 다음 코드처럼 배열에 명시하기만 하면 된다.

이 예에서는 인덱스 4개(1, 0, 3, 0)이 한 번에 추출됐다. 이처럼 인수에 배열을 사용하면 여러 행도 한꺼번에 추출할 수 있고, 참고로 이는 미니배치 처리를 가정했을 경우의 구현이다.
그럼 Embedding 계층의 forward() 메서드를 구현해보자.

이 책의 구현 규칙에 따라 인스턴스 변수 params와 grads를 사용한다. 또한 인스턴스 변수 idx에는 추출하는 행의 인덱스(단어ID)를 배열로 저장한다.
이어서 역전파를 생각해보자. Embedding 계층의 순전파는 가중치 W의 특정 행을 추출할 뿐이다. 단순히 가중치의 특정 행 뉴런만을 다음 층으로 흘려보낸 것이다. 따라서 역전파에서 앞 층(출력 측 층)으로부터 전해진 기울기를 다음 층(입력 측 층)으로 그대로 흘려주면 된다. 다만, 앞 층으로부터 전해진 기울기를 가중치 기울기 dW의 특정 행(idx번째 행)에 설정한다.
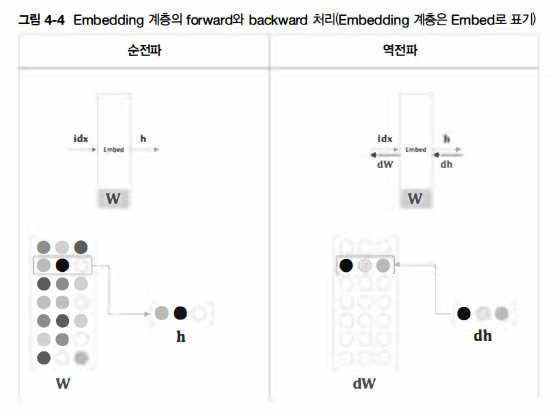
이 그림을 기초로 backward()를 구현해보자.

다음과 같이 가중치 기울기 dW를 꺼낸 다음, dW[...]=0 문장에서 dW의 원소를 0으로 덮어 쓴다. (dW 자체를 0으로 설정하는 게 아니라, dW의 형상을 유지한 채 그 원소들을 0으로 덮어쓰는 것이다) 그리고 앞 층에서 전해진 기울기 dout을 idx번째 행에 할당한다.
그런데 앞의 backward() 구현에는 사실 문제가 하나 있다. 그 문제는 idx의 원소가 중복될 때 발생한다. 예컨대 idx가 [0, 2, 0, 4]일 경우를 생각해보면 아래 그림과 같은 문제가 생긴다.
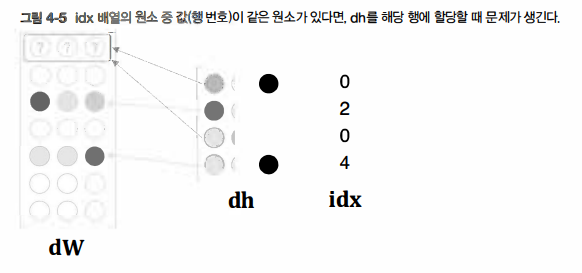
그림과 같이 dh의 각 행 값을 idx가 가리키는 장소에 할당해보면, dW의 0번째 해에 2개의 값이 할당되어 먼저 쓰여진 값이 덮어쓰여진다. 이 중복 문제를 해결하려면 '할당'이 아닌 '더하기'를 해야 한다. 즉 dh의 각 행의 값을 dW의 해당 행에 더해준다.

여기서는 for문을 사용해 인덱스에 기울기를 더했다. 이것으로 idx에 중복 인덱스가 있더라고 올바르게 처리된다. 이상으로 embedding 계층을 구현해보았다. word2vec(CBOW 모델)의 구현은 입력 측 MatMul 계층을 Embedding 계층으로 전환할 수 있어, 메모리 사용량을 줄이고 쓸데없는 계산도 생략할 수 있게 되었다.
4.2 word2vec 개선 2
이어서 word2vec의 두 번째 개서능ㄹ 진행해보자. 남은 병목은 은닉층 이후의 처리(행렬 곱과 Softmax 계층의 계산)이다. 이 병목을 해소하는 게 이번 절의 목표인데, 바로 네거티브 샘플링 기업이다. 이는 어휘가 아무리 많아져도 계산량을 낮은 수준에서 일정하게 억제할 수 있다.
4.2.1 은닉층 이후 계산의 문제점
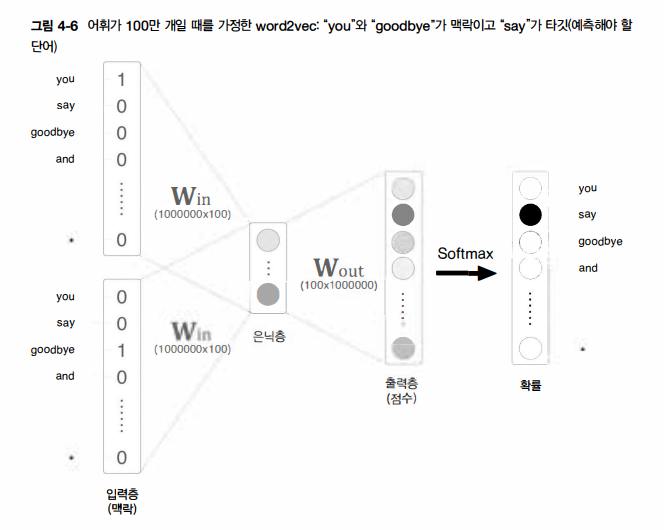
위 그림에서 보듯, 은닉층 이후에서 계산이 오래 걸리는 곳은 다음 두 부분이다.
1) 은닉층의 뉴런과 가중치 행렬(Wout)의 곱
2) Softmax 계층의 계산
첫 번째는 거대한 행렬을 곱하는 문제 행렬 곱을 '가볍게' 만들어 줘야 한다. 두 번째로 Softmax에서도 같은 문제가 ㅂ라생한다.
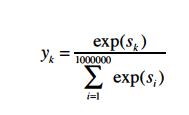
위 식은 Softmax 식으로 k번째 원소(단어)를 타깃으로 했을 때의 식이다. 이 식에서 어휘 수를 100만개 가정했으므로 분모의 값을 얻으러면 exp계산을 100만 번 수행해야 한다. 어휘 수에 비례해 증가하므로 Softmax를 대신할 '가벼운'계산이 필요하다.
4.2.2 다중 분류에서 이진 분류로
네거티브 샘플링 기법에 대해 설명하자면, 이 기법의 핵심은 '이진 분류'에 있다. 더 정확하게 말하면 '다중 분류'를 '이진 분류'로 근사하는 것이 중요 포인트이다.
'Data Science > NLP' 카테고리의 다른 글
| 밑바닥부터시작하는딥러닝3 - word2vec (0) | 2022.02.04 |
|---|---|
| [밑바닥부터시작하는딥러닝2] Chapter2 - 자연어와 단어의 분산 표현 (0) | 2022.02.03 |
| NLP(자연어처리) - 자언어처리란? intro (0) | 2021.02.14 |
| NLP(자연어처리) - 정규표현식 with python (2) (0) | 2021.02.14 |
| NLP(자연어처리) - 정규표현식 with python (1) (0) | 2021.02.14 |

최근댓글